Posts

, ,

Learning How Delta Creates Profits When Trading Gold

Last week’s articles focused specifically on the option Greek Theta. This week we will shift gears and adjust our focus on Delta, another fundamental tenet of option trading. The official definition of Delta as provided by Wikipedia is as follows:

?, Delta – Measures the rate of change of option value with respect to changes in the underlying asset’s price.

Delta has a significant impact on the price of an option contract(s). When a trader is long a call contract, Delta will always be positive. Likewise, if an option trader owns a put contract long, Delta will always be negative. As option contracts get closer to the money their Delta increases causing the option contract to rise in value rapidly as the option gets closer to being in the money.

Clearly Theta has an adverse impact on a trader who is long a single options position (own options long with no hedge or spread), however Delta is extremely dynamic and is one of the major factors directly responsible for option pricing as the price of the underlying changes throughout the trading day.

If an option is deep in the money, the option contract will have a higher Delta and will generally act similarly to actually owning the individual stock. For a deep in-the-money GLD call that has a Delta of +.80, the first dollar GLD rises by then the value of the GLD call options increases by roughly $0.80 or $80.

If the delta is 0.80, this essentially means that the GLD call option will increase in value 0.80 ($80) for every $1 that the GLD ETF increases. As the GLD option goes deeper into the money, the Delta will typically rise until it nearly produces the same gains as the GLD ETF until the delta asymptotically approaches 1.00 and the option moves in lockstep with the underlying. While my next article will continue to help explain Delta, it is important to understand how Delta can enhance a trader’s return when trading options with a specific directional bias.

While options exist for the gold futures contract, typically if I want to trade gold I utilize the GLD ETF. The primary reason is that the ETF offers liquid options, which makes it easier to initiate spreads and multi-legged orders. If options are thinly traded, the bid ask spread is almost always wide making it more difficult to get a good fill and a good overall price. Most option traders stay away from underlying stocks that have illiquid options.

In order to better illustrate how an options’ Delta can create profits, I will use GLD as an example. Keep in mind, I am not advising any traders to buy or sell options naked. I only trade options using strategies that help mitigate various risks to my capital. Theta (time) risk, volatility risk, and market risk are not being considered as this is merely an example to illustrate the power of Delta.

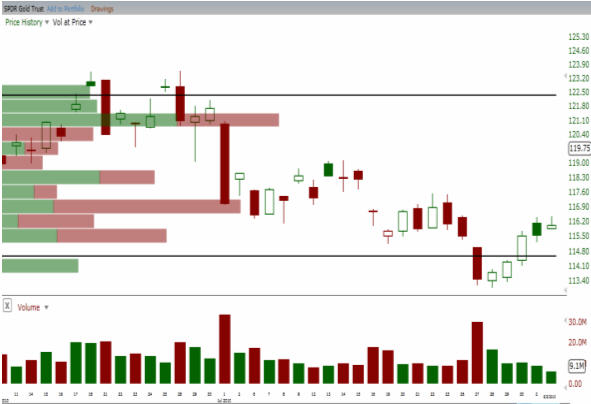
Recently Gold and subsequently GLD suffered a pretty significant pullback. GLD broke down through a major horizontal trend line and the daily chart was extremely bearish. Just when a lot of traders were preparing to get short GLD, buyers stepped in and pushed GLD’s price back above the support area. The GLD daily chart listed below illustrates the breakdown and subsequent failure and a powerful rally followed.

Let us assume for contrast that an option trader and an equity trader each want to get long GLD. The equity trader buys 200 shares of GLD at $115/share. Assuming the equity trader does not use margin, the total trade would cost around $23,000 not including commissions. The option trader decides to utilize delta and purchases 5 October 107 calls which in our example cost $900 per contract for a grand total of $4,500 not including commissions.

We will assume the October 107 calls have a Delta of 1.00. When a call option has a delta of 1.00, it essentially means that the owner of the call is going to get 100% of the move reflected in the premium of the option he/she owns. Thus if GLD increases by $1, the value of the option would increase $1 all things being held constant.

This is where Delta really shines; it shines even brighter than gold in this illustration. Both the equity trader and the option trader have a profit target of $118/share. A few days later GLD reaches $118/share and both traders close their trades with profits. The equity trader made $3/share which relates to a total gain of $600, or around 2.60%.

The option trader realized roughly 95% of the move, meaning around $2.85. The option trader had five total contracts for a total gain of $1,425 less commissions. The total gain for the options trader was over 31% less commissions.

Keep in mind, the option trader only had $4,500 of maximum risk while the equity trader was risking over $20,000. The option trader made over 100% more money, while risking only 25% of the total capital required by the equity trader. Behold, the power of Delta!

Learn more about how to find low risk options trades and get our alerts at: www.OptionsTradingSignals.com

J.W. Jones is an independent options trader using multiple forms of analysis to guide his option trading strategies. Jones has an extensive background in portfolio analysis and analytics as well as risk analysis. J.W. strives to reach traders that are missing opportunities trading options and commits to writing content which is not only educational, but entertaining as well. Regular readers will develop the knowledge and skills to trade options competently over time. Jones focuses on writing spreads in situations where risk is clearly defined and high potential returns can be realized.

GET MY FREE OPTIONS TRADING REPORTS TO YOUR INBOX

, ,

Learning How to Profit from Theta When Trading SPX Options

J.W. Jones
As discussed in the first article, “The Hidden Potential of Learning How to Trade SPX and Gold Options” I pointed out that there are several fundamental principles that must be mastered before profits can be attained when trading options. Novice traders typically skip the discussion about “The Greeks” and skim over volatility only to watch their precious trading capital disappear.

As promised, this article and future articles are going to discuss the Greeks as they relate to options trading in a way that hopefully everyone reading this can understand. While there are more than ten Greek symbols that directly relate to option pricing, an option trader must be able to clearly articulate and understand 4 of the ancient Greek symbols and one English invention. (Vega is not a true Greek symbol-Look it up!)

The five core Greek symbols which are critical in order to understand are as follows, in no particular order: Delta, Theta, Vega, Gamma, & Rho. Most veteran option traders have a sound understanding of Delta, Theta, Vega, & Gamma. Rho is not nearly as well known, but anyone who has ever studied econometrics, option pricing models, or has studied applied finance know all too well the importance of Rho. For inquiring minds, Rho measures sensitivity to current interest rates.

Today’s article is going to focus on the Greek symbol Theta. By now many readers may wonder why I continually capitalize the Greek symbols, and the reason is because they are that critical. The technical definition of Theta derived directly from Wikipedia when applied to options is as follows:

THETA – T, measures the sensitivity of the value of the derivative to the passage of time: the “time decay.”

Time decay (Theta decay) is of critical importance when an option trader is attempting to quantify and/or mitigate risk. There are two parts factored into the price of an option contract: extrinsic value (a major component of extrinsic value is Theta; the other is implied volatility) and intrinsic value which would be the amount of money a trader would gain if they exercised an option right away. A great many authors who opine about options get caught up using terminology like intrinsic and extrinsic value which only serves to confuse most novice option traders even more. I refuse to use those words in my writing as I find them to be cumbersome and option trading can be made much more difficult than it needs to be.

Theta and time decay are synonyms when discussing options. An easy way to remember their congruence is that the word time starts with a “T” as does Theta. If a trader owns calls or puts outside of any type of spread, they are totally exposed to time decay (Theta) and as an option contract gets closer to expiration, the time value of the contract diminishes. This accompanied with failure to account for implied volatility (to be discussed in the future) are the fundamental reasons why so many people lose money when trading options.

Just as theta can be an option trader’s worst enemy, it can also be used as a profit engine. If an option trader sells an option contract to open the position, that option trader is using theta as a method to profit or as a way to reduce the cost of a spread. While this article will not spend a ton of time discussing various option spread techniques, in the future we will discuss them in detail. At this point, we are only attempting to understand that Theta represents the time decay priced into an option.

It is also critical to understand that Theta (time decay) is not linear in the time course of the life of an option and accelerates rapidly the final two weeks before an option expires. The rapid time decay the final two weeks before expiration presents a multitude of ways to drive profitability, but it also can represent unparalleled risk. While this article is just an introduction to Theta, the next article later this week will continue the time decay discussion.

Since we are discussing Theta, I thought it would make sense to discuss a trade I took last week which utilized Theta as the profit engine. Recently a variety of underlying indices, stocks, and ETF’s have options that expire weekly. Weekly expiration expedites Theta and gives option traders additional vehicles to produce profits.

While most equity or futures traders might shy away from a chart like this, an option trader has the unique ability to place a high probability trade. I believed that the market would stall around the SPX 1130 area so I looked for a trade which would utilize the SPX weekly options. The SPX weeklies expire based on the Friday SPX open. With the SPX trading around 1124, I put on a call credit spread which used time decay as the primary profit engine.

The setup I used involved selling an 1150 SPX call and buying an 1175 SPX call, which is also known as a vertical credit spread. I received $100 (1.00) for the 1150 SPX call and purchased the 1175 call for $20 (0.20). The $80 dollar profit represents the maximum gain per contract sold. As an example, if I placed this trade utilizing five contracts per side I would have a maximum gain of $400 dollars. The probability of success at the time when I placed this trade was around 78% based on a log normal distribution of the price of the underlying.

Immediately after placing the trade I utilized a contingent stop order that would close my trade entirely if the SPX reached the 1135.17 area. Essentially, my maximum loss not including commissions was limited to around $60 dollars per contract with a maximum gain of around $80 per contract assuming we did not get a big gap open.

Essentially, if the SPX stayed below 1135.17 for two days and opened on Friday below the 1150 level my trade would reach maximum profitability. This is a trade I actually placed on Tuesday afternoon, however I exited the position before the close on Thursday due to the impending jobs report which was set to come out Friday morning. I was able to collect over 60% of the premium sold per contract ($80) which came to about $45-50 per side. At $1,000 dollars risked based on my stop level, the trade would have produced a net gain of around $750 dollars in less than 3 days.

Hopefully this basic example illustrates the potential profits options can produce if they are traded appropriately with risk clearly defined while having hard stops in place. This trade produced a nice profit, however it was susceptible to a gap open, thus I maintained a relatively small position to mitigate my overall risk profile. As always, a trader must see potential risks from all angles and utilize proper money management principles when determining how much capital to risk. In closing, I will leave you with the insightful muse of famed trader Jesse Livermore, “A loss never troubles me after I take it.”

If you would like to continue Learning about the Hidden Potential Pptions Trading Can Provide please join my FREE Newsletter: www.OptionsTradingSignals.com

J.W. Jones is an independent options trader using multiple forms of analysis to guide his option trading strategies. Jones has an extensive background in portfolio analysis and analytics as well as risk analysis. J.W. strives to reach traders that are missing opportunities trading options and commits to writing content which is not only educational, but entertaining as well. Regular readers will develop the knowledge and skills to trade options competently over time. Jones focuses on writing spreads in situations where risk is clearly defined and high potential returns can be realized.

LEARN MORE ON OPTIONS AND GET NOTIFIED ABOUT UPCOMING TRADING SERVICE